Introduction
Sunkens have a pity system now, so we need to figure out a new best fishing strategy to be prepared for the release of AO. Actually, no, the release is a long way ahead and fishing is boring, but I’m also bored so I’ll make a long winded post pretending it matters.
Methodology
We need a way to find the average number of catches required to catch a sunken item. One of the ways to do that is the following:
Suppose you’re fishing for sunkens, every catch has a 1/2000 chance to be a sunken, and you stop fishing once you catch one. We then know that there is a 1/2000 chance that you stop fishing after every catch, in case you caught a sunken, but you would have only gotten so far if you haven’t caught one yet.
So, the probability of stopping after a random catch is the probability of catching a sunken, in this case 1/2000, multiplied by the probability that you haven’t caught one in any of the previous tries. If we then sum all possible numbers of tries, each multiplied by the probability that you caught a sunken on that specific try (that is the probability of catching a sunken multiplied by the probability of not catching one in all the previous tries, yada yada, you understand this now), we would get the average number of tries needed to catch a sunken. Let’s formalize that a bit.
Let the probability of catching a sunken be 1/x, the probability of not catching one would then be 1 - 1/x, since you either get one or you don’t, and the probability of 1 means something is sure to happen.
If the probability for an event to happen is p, then the probability of it happening twice in a row is p*p, and for it to happen n times in a row would then be pn. The probability of not get a sunken n times in a row would then be (1 - 1/x)n.
The probability to catch a sunken in exactly n tries would therefore be 1/x * (1 - 1/x)n-1.
The average number of catches after which you would get a sunken would then be the limit as n approaches infinity of the following series:
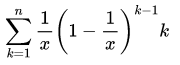
If you are interested, you could prove that this is actually equal to x, but I’m not going to do that since it’s not needed and I’d rather l̷̙̓ê̶̛̖å̵̮͠v̶̢͗ê̸̗̇ ̵̢͋ï̶̗͘†̵͈͂ ̶̥̔å̴̩̂§̴̝̌ ̴̈͜å̴̞͝ñ̴̬̏ ̵̯́ê̴͉̾x̶̯̚ê̶̪͆ṙ̷̬¢̴̨̎ï̶̻̉§̷̺̈́ê̸̯͝ ̵͓̃†̶͕̊ð̸̢̕ ̶͔̑†̵͖̓ẖ̸͝ê̸͘͜ ̴̹͐r̶͍̉ê̵̩̑å̷͓̚Ð̶̹̓ề̴̡r̷̹̎r̴̨̡̛̩͉̹̠̦͕̹̻̄̂́̄̈́́̓͛́.
In our case, we’re going to use this formula up to 2999, since when you reach 3000 tries you would get a sunken automatically. The result we need is this one:
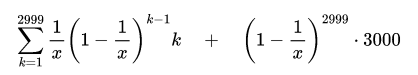
I made this here program to calculate that for me, and do it in respect to the item chance stat of a fishing rod:
#include <stdio.h>
int main(int argc, char *argv[])
{
long double ItemChanceStat[5] = {0.8L, 1.0L, 1.05L, 1.25L, 1.5L};
for(int i = 0; i < 5; i++)
{
long double EndChance = (1.0L / 2000.0L) * ItemChanceStat[i];
long double ArrivalChance = 1.0L;
long double WeightedSum = 0.0L;
for(int j = 1; j < 3000; j++)
{
WeightedSum += ArrivalChance * EndChance * j;
ArrivalChance *= (1.0L - EndChance);
}
WeightedSum += ArrivalChance * 3000.0L;
printf("Item chance stat: %Lf; Average catches for sunken: %Lf; Average sunkens per catch: %Lf\n", ItemChanceStat[i], WeightedSum, (1.0L / WeightedSum));
}
return 0;
}
After getting that, we just need to take into account the time it would take to reach this number of tries and get your sweet, sweet, sea salted sunken.
We simply multiply a fishing rods Lure stat with the Average sunkens per catch we got, se we get a score measured in sunkens/time, that we can also multiply by 1000 just to make it look better and since it’s relative anyways.
Results
| Item chance | Average catches for sunken | Average sunkens per catch |
|---|---|---|
| 0.8 | 1747.195213 | 0.000572 |
| 1.0 | 1553.907052 | 0.000644 |
| 1.05 | 1510.624846 | 0.000662 |
| 1.25 | 1354.775841 | 0.000738 |
| 1.5 | 1192.919617 | 0.000838 |
| Fishing Rod | Item chance | Lure | Sunken over time score |
|---|---|---|---|
| Magnetic Collectors | 1.5 | 0.8 | 0.6704 |
| Luring Collectors | 1.25 | 1.05 | 0.7749 |
| Magnetic Bronze | 1.05 | 1.25 | 0.8275 |
| Luring Bronze | 0.8 | 1.5 | 0.858 |
Conclusion
Use a Luring Bronze Rod.
